Bynomial Code

This post introduces a relatively new algorithm, along with an open-source demo iPad app, that can pre-process a large set of numeric data to help perform extremely fast error-tolerant lookups at query time.

Problems you can solve

There is a class of algorithms known as locality-sensitive hashing (LSH) algorithms; this is a new one of those.  They were pioneered by Rajeev Motwani and Piotr Indyk, who remains one of the primary world experts.  LSH algorithms can be used to help solve the nearest neighbors problem.  Solving this problem, which I’ll describe a little more below, is still the most obvious way to use LSH algorithms, along with the similar k-nearest neighbors problem.

The nearest neighbor  (NN) and k-NN problems

The nearest neighbor question is this: Given a large set of points (P), pre-process it so that later, when you receive a new query point (q), you can very quickly return the subset of original points P which are within a fixed radius r of q (the desired output is the set near(q, P) = {p in P : ||p – q|| < r}).  The radius r is chosen in advance and doesn’t change, although you can store different outputs of the pre-processing which can handle multiple radii.  Technically speaking, the NN problem actually asks for the single point in P closest to q, and the k-NN problem asks for the k points in P closest to q; we introduce the different version with the radius because it is close enough for practical purposes, and is more directly solved by LSH algorithms.

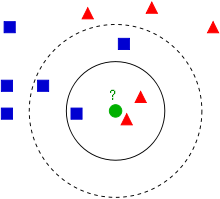
Stuff you can do with NN or k-NN

Unless you’re a quasi-academic algorithm junkie like me, your eyes probably glazed over a little in that last paragraph.  Despite sounding abstract, these problems have a myriad of very real applications.

Recommendations

For example, let’s say you have a user database with usage data per user, such as ratings from netflix or yelp users.  Temporarily forgetting about missing fields (that’s a somewhat independent challenge), you could represent every user as a vector, and then quickly find each user’s 10 “nearest neighbors,” which in this case means the 10 other users most like the query user.  From there, you can combine those 10 users to get a reasonable guess at what else the query user likes, and recommend the guessed-as-highly-rated items to the query user (excluding things they’ve already rated).

Handwriting recognition

Written characters can be encoded as an image, and images can be further reduced in a way that allows for some rotations and skews to get a relatively small thumbnail – let’s say at 500 coordinates, each a float arrived at by some function of a small black & white image.  If you made the thumbnails well, then slightly different ways of writing the number ‘7’ will result in slightly different – but mostly similar – thumbnails.  As vectors, they will be close together.

Later you get a new image as input, and your job is to figure out what character it is.  You get the thumbnail in the same way, and now just do a quick lookup via LSH and return the most-common character in that set.  (This general method can actually be used for any machine learning classification problem.)

Duplicate detection

Suppose you’re a site like youtube with user-generated content and copyright lawyers at other companies who are feeling sue-happy.  Your job is to quickly and efficiently find any user-uploaded videos that violate copyright.  You have a database of known-copyright material, but the tricky part is that users will mess with these videos in small ways so that they are never exact copies.

LSH to the rescue!  Because any LSH-based lookup is automatically error tolerant, the copies don’t have to be exact matches.  You can choose a meaningful threshold for what it means to be a “copy,” or perhaps simply flag a possible copy for further scrutiny with a slower algorithm.

Fraud detection

This case is theoretically similar to handwriting recognition.  Suppose you’re a bank or credit card company, and you want to figure out as quickly as possible when a credit or debit card is stolen.  Just as in the handwriting case, you have a set of sample data (which would look like times, locations, and purchase prices with numerical categories), and you do an LSH lookup for the nearest usage cases; you might also want to use thumbnails that can better match the numerically-close scale with the fraud-valid scale.

I could go on for a while.  Basically anything with numeric data that also involves some error-tolerance, a lot of data to go through or large data points (like videos), and the need for speed.

How it works

The full details are left to other places, such as the paper and slides below; but here is the basic idea:

An LSH approach is like asking a group of people to write down their zip codes.  You keep a zipcode/name table sorted by zip code.  When a new person arrives, you ask their zip code, and do a quick look in the table and can tell them who lives near them.

The zip code function is a real-life locality sensitive hash.  It has these properties:

• It’s a mapping from data to a discrete (non-continuous) set
• Data points (people) with the same hash value (zip code) tend to live close together

This is nice because it allows for fast lookups.  So far this describes the general LSH idea, which is not new.

What is new in this algorithm is how it computes the hash values.  Instead of relying on dimension reduction, it relies on using a tessellation (tiling) of d-dimensional space with one shape.  First imagine this shape is a hypercube (d-dimensional cube), so we have a fixed grid of cubes in space.  If we turn every corner into a hash table bin, then each hypercube will be thought of as a neighbor of each adjacent cube.  In other words, every corner of every cube gets its own zip code, and we call two people neighbors if any of their many zip codes match.

But this idea by itself is very bad for high dimensions – it is attacked by the curse of dimensionality.  The number of corners is 2^d, and the number of neighboring hypercubes is 3^d-1.  So the cost for us is exponentially-many hash outputs of every point, and the gain is that we can match exponentially-many neighboring shapes (hypercubes).

The new algorithm solves this by using a simplex to tile space.  A simplex is a d-dimensional triangle; so it has d+1 corners in d dimensions.  Now we pay the cost of having linearly-many hash outputs of every point with the gain of super-exponentially-many neighboring shapes!  Compared to the hypercube approach, it is a clear win.

The iPad app

The iPad app demonstrates the 2d version of the algorithm.  It generates a set of random points, and plots these on the screen.  When you touch the screen, it connects your fingertip to the neighbors found by the LSH algorithm.  It also can display the proximity graph found during preprocessing, and allow you to switch on/off the skew correction component of the algorithm (it’s generally more accurate while on).

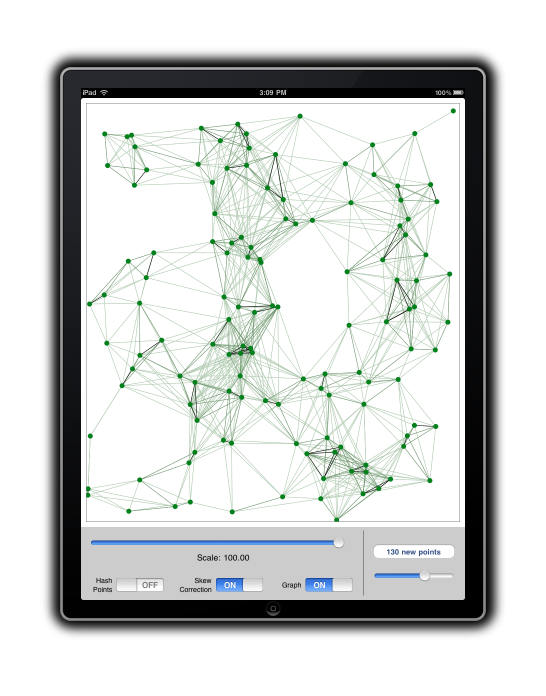
The code for this app is open source under the Apache 2 license, and currently hosted as ipadlocalityhash on google code.

Source & References

The official open-source version of the demo code can be found here:

http://code.google.com/p/ipadlocalityhash/

If you want to skip a couple links, you can also download the xcode project source (for v1.0) right here:

ipadlocalityhash.tar.gz

Finally, here are links to the original paper describing the algorithm, and some slides I recently used to present it (with the help of this demo app):

https://www.siam.org/proceedings/soda/2010/SODA10_094_neylont.pdf

http://wiki.hackerdojo.com/f/lsh_hacker_dojo_talk.pdf